
The Good, the Bad and the Ugly in the CDC's Face Mask Study
They could have used more appropriate models and they should have accounted for political partisanship.
While perusing the news, I read eagerly about the CDC’s recent study examining associations between county-level mask mandates and COVID-19 growth rates. This study has already been the subject of angry retorts from the restaurant industry due to the CDC’s claim that restaurant closures reduced COVID-19 spread. Looking at the underlying details in the study, though, revealed some concerns about the particular model they used, known as a two-way fixed effects model, and also an important factor they left out of the model entirely: political partisanship.
To examine these deficiencies, I replicated their model from scratch and also employed different panel data models to provide clearer answers. In brief, the negative association between mask mandates and the spread of COVID-19 does hold up, but it appears to be highly conditional on partisanship. In addition, there are a lot of complexities when it comes to comparing counties, and I do not believe the CDC or anyone else has yet resolved all of them. So while I applaud the CDC for doing a lot of hard work on data collection, we still have a ways to go before we can fully understand how effective mask mandates were against COVID-19.
In this post I first discuss my challenges replicating their analysis, and then I critique the choices they made in their paper. Later I put forward my own analysis to probe in more detail the role of mask mandates. I include the code I use to estimate models in this blog post to be transparent about how I did the re-analysis. If you are not familiar with R code, feel free to skip those sections.
If you would like access to the code and data I used to write this blog post, please use this Github repository.
Collecting the CDC Paper’s Data
The first and most necessary step to replicate the CDC’s findings is to obtain data to fit their model. This exercise is also important because it shows if 1) their article is clear enough to successfully re-trace their steps and if 2) all the data is available to do so. The authors of the study have posted their mask and other county policy data online, which was easy to download and analyze. Unfortunately, some of their data, particularly testing and case data collected by Health and Human Services (HHS), is not available to the wider public. Given the new administration’s commitment to transparency, it really should be available publicly. Because I am writing a blog post and wanted data I could share, I chose instead to use open source repositories of case and test data, specifically the New York Times for county-level cases and the COVID-19 Tracking Project for test data by state. Because I could not find testing at the county level, I approximated tests by county by multiplying that county’s share of state COVID-19 tests with that state’s daily testing total.
There were some ambiguities in interpreting the article’s instructions about the CDC’s county policy data. The policy restrictions, including stay-at-home orders, mask mandates, and restaurant and bar closures, have multiple categories, such as partial enforcement, and it was not clear if I should use all the categories or collapse them to binary indicators. This became an issue later in the model because some of the categories were collinear and the model dropped them, particularly bar closures. I am not sure for that reason if my use of the CDC’s data exactly matches theirs.
Replicating the CDC’s Results
Given these caveats about data collection, the model estimates I obtained using the same specification–two-way fixed effects for county and day–are broadly similar to their estimates, although the associations are weaker on average. I also used the same comparison periods they describe in the paper. For each county, I selected the first twenty days preceding the mask mandate implementation, and then fit separate models to five different post-mandate periods: 1-20 days following the mandate, 21-40 days, 41-60 days, 61-80 days, and 81-100 days. The ambiguity that surfaced while doing this occurred in counties with multiple periods of mask mandates: what if there weren’t twenty days prior to the second mask mandate? I included as many as were available, but its still important to note this ambiguity as it is not clear exactly what data coding the CDC used.
The plot below compares my estimates of the effect of mask mandates to theirs by the five different post-mandate time periods. The weaker associations in my estimates could simply be due to measurement error from using unofficial sources, so the smaller effects are not necessarily a huge concern (though it would be better if the CDC released all of the data they used). On the whole, I think this replication was at least partially successful as the confidence intervals of the estimates overlap.
The following code replicating the CDC’s paper is quite long but is included for transparency’s sake. I used the fixest package with R to fit linear models due to the scale of the data and the number of fixed effects (one for each county plus one for each day).
# estimate CDC model using lm
# baseline = 1-20 days before implementation
# models differentiated by number of days included post-implementation
# note: no mention of whether this makes the panel imbalanced
# a bit odd too if there are multiple times that county switches in and out of mask mandates
d1 <-
filter(combined_data,
(n_day_before > 0 &
n_day_before < 21) |
(n_day_after > 0 &
n_day_after < 21)) %>% fixest::feols(
cases_diff_log ~ mask_status + test_prop + stay_status + rest_action + bar_order + ban_gather |
fips + date,
data =
.,
cluster =
"FIPS_State",
weights =
~ pop
)
d2 <-
filter(combined_data,
(n_day_before > 0 &
n_day_before < 21) |
(n_day_after > 20 &
n_day_after < 41)) %>% fixest::feols(
cases_diff_log ~ mask_status + test_prop + stay_status + rest_action + bar_order + ban_gather |
fips + date,
data =
.,
cluster =
"FIPS_State",
weights =
~ pop
)
d3 <-
filter(combined_data,
(n_day_before > 0 &
n_day_before < 21) |
(n_day_after > 40 &
n_day_after < 61)) %>% fixest::feols(
cases_diff_log ~ mask_status + test_prop + stay_status + rest_action + bar_order + ban_gather |
fips + date,
data =
.,
cluster =
"FIPS_State",
weights =
~ pop
)
d4 <-
filter(combined_data,
(n_day_before > 0 &
n_day_before < 21) |
(n_day_after > 60 &
n_day_after < 81)) %>% fixest::feols(
cases_diff_log ~ mask_status + test_prop + stay_status + rest_action + bar_order + ban_gather |
fips + date,
data =
.,
cluster =
"FIPS_State",
weights =
~ pop
)
d5 <-
filter(
combined_data,
(n_day_before > 0 &
n_day_before < 21) | (n_day_after > 80 & n_day_after < 101)
) %>%
fixest::feols(
cases_diff_log ~ mask_status + test_prop + stay_status + rest_action + bar_order + ban_gather |
fips + date,
data = .,
cluster = "FIPS_State",
weights = ~ pop
)
# combine data from all models together into a tibble
all_coefs <- lapply(list(d1,d2,d3,d4,d5),function(d) slice(summary(d)$coeftable,1)) %>%
bind_rows %>%
mutate(Model=c("1-20 Days",
"21-40 Days",
"41-60 Days",
"61-80 Days",
"81-100 Days"),
upb=Estimate + 1.96*`Std. Error`,
lb=Estimate - 1.96*`Std. Error`,
Type="Replication")
# combine with original estimates
all_coefs <- bind_rows(all_coefs,
tibble(Estimate=c(-0.5,-1.1,-1.5,-1.7,-1.8),
lb=c(-0.1,-0.6,-0.8,-0.9,-0.7),
upb=c(-0.8,-1.6,-2.1,-2.6,-2.8),
Model=c("1-20 Days",
"21-40 Days",
"41-60 Days",
"61-80 Days",
"81-100 Days"),Type="CDC"))
all_coefs %>%
ggplot(aes(y=Estimate,x=Model)) +
geom_pointrange(aes(ymin=lb,ymax=upb,colour=Type),
position=position_dodge(width=0.5),
fatten=2) +
geom_text(aes(label=round(Estimate,digits=2),group=Type),
position=position_dodge(width=0.5),
size=3,vjust=-.75) +
geom_hline(yintercept=0,linetype=2) +
theme_tufte() +
geom_vline(xintercept=0,linetype=2) +
scale_colour_viridis_d() +
coord_flip() +
scale_y_continuous(labels=scales::percent_format(scale=1)) +
labs(x="Comparison Period",y="Percentage Change in Daily COVID-19 Cases") +
ggtitle("Replication of CDC Mask Results with Open Source Data")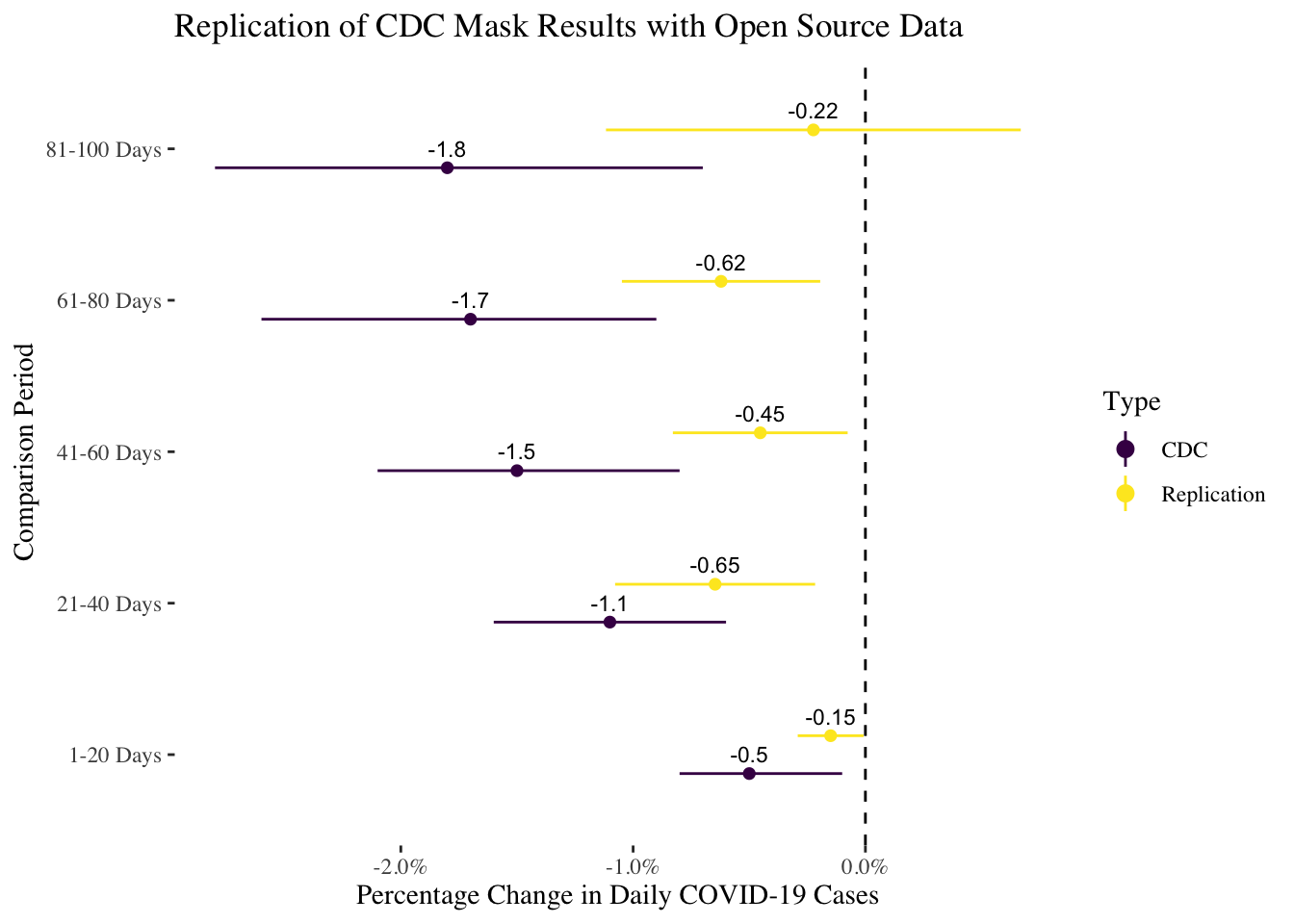
Issues with the CDC’s Analysis
Given the reasonably successful replication, I now turn to some of the issues with the analysis. One peculiar choice they made was to subdivide their data into the different days following a mask mandate as the plot above shows. The reason for this choice, though they did not discuss it in their paper, is probably due to the difficulty in comparing COVID-19 case rates across counties. It is quite likely that counties will wait to adopt mask mandates until COVID-19 rates are very high, so the unconditional association between mask mandates and COVID-19 could end up being strongly positive. This issue can be seen in the plot below, where I show each county’s COVID-19 growth rate by day, and colour the lines by whether a mask mandate was enforced. As can be seen, the imposition of mask mandates begins later in the course of the pandemic around March and April as case rates pick up and the CDC issues mask-wearing guidance.
# plot the orders as line plots to show when the tend to be implemented
combined_data %>%
ggplot(aes(y=cases/pop,x=date)) +
geom_line(aes(colour=mask_status,group=fips),alpha=0.5) +
theme_tufte() +
scale_color_viridis_d() +
labs(x="",y="Percent of County Infected with COVID-19",
caption="COVID-10 cases data from the New York Times and mask mandate data from the CDC.") +
scale_y_continuous(labels=scales::percent) +
ggtitle("County COVID-19 Infection Rates Over Time")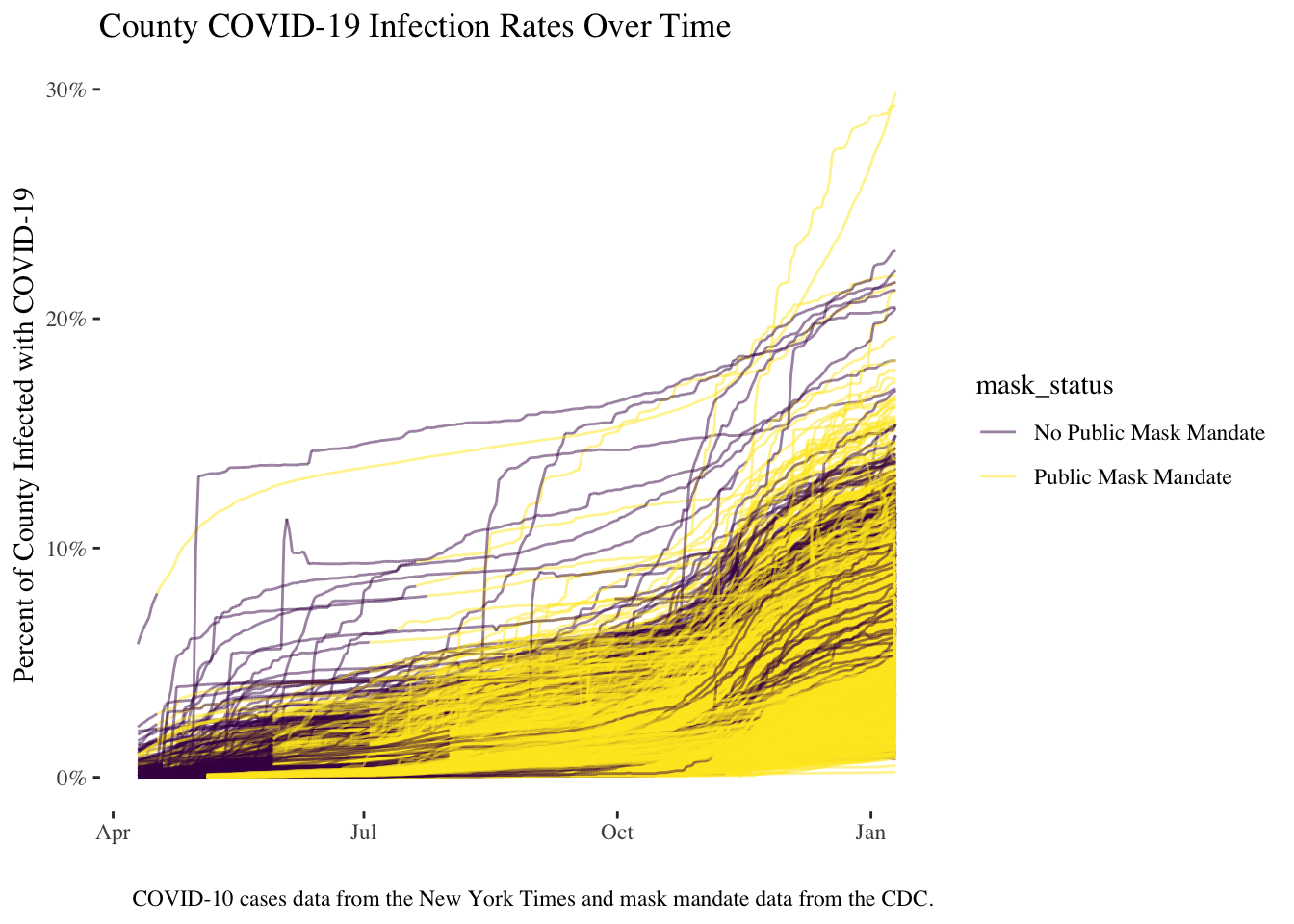
The CDC tried to resolve this by restricting their sample to the twenty days preceding a mask mandate and one of the five categories mentioned before for twenty-day periods following the mask mandate. This is one approach, but not a particularly satisfying one. The day cutoffs are very arbitrary (why twenty-day intervals? Why only the previous twenty days before a mask mandate?). I think a much better approach, and one I show later, is to try to control for some of the differences that may lead to mask adoption, and to use all the sample data unless there is a very clear reason not to.
However, there is an even more significant concern, and that is the modeling approach itself. The CDC used a linear model with fixed effects for both days and counties, or what is commonly known as a “two-way” fixed effects model. This would be the equivalent of having a dummy/binary variable in the model for each county and day separately, or 3477 additional variables. This stunning number should give us pause: what is the point of adding thousands of variables to the model? The resulting linear model is so big that R’s default linear model function lm could not estimate it, requiring me to use the fixest package which is more memory efficient. What is happening to our interpretation of mask mandates by including so many extra variables?
I’ve written a previous blog post about the two-way fixed effect model and panel data models in general, following on a paper I wrote with Jon Kropko on the topic, which I refer to the reader to a fuller answer to these questions. Our research and an increasing number of papers question whether the two-way fixed effects model does what people say it does, which is control for a wide array of possible omitted variables.
The problem is that fixed effects are not, on their own, some magic formula to get rid of inferential problems. Including fixed effects can help isolate one of two dimensions in the data: 1) variation in COVID-19 growth rates within counties over time (what the plot above shows) or 2) a cross-section of county growth rates for a given day. The first corresponds to including a dummy variable for each county, and the second including a dummy variable for each day.
In general, both of these comparisons are potentially interesting. Looking at growth rates within counties implies that we think COVID-19 growth rates following the introduction of mask mandates will fall. However, this comparison can be difficult because we know there are a lot of other factors that change over time within counties, such as people’s increasing awareness of the effectiveness of masks. Similarly, we would think that if mask mandates are effective, counties with mandates on a given day should have lower growth rates than counties without mandates (the cross-section). Of course, differences across counties can affect these comparisons, especially if there are reasons why some counties may want to adopt and enforce mask mandates more than others.
The CDC, though, included both kind of fixed effects, which makes it very hard to know what comparison they are trying to draw. In the blog post mentioned above, I show why this particular estimate is nearly impossible to understand. It would seem the CDC is to trying to address all possible inferential issues by including a cornucopia of fixed effects, but fixed effects only enable the researcher to draw comparisons, not remove all sources of bias. To deal with the possible factors that might affect our estimates, we need to think about including data that measures potential confounding variables, not just including as many fixed effects as possible and hoping for the best.
To illustrate this, I replicate the CDC’s analysis except that I compare a model with fixed effects for counties (within-country variation), a model with fixed effects for days (cross-sectional variation), and plot them next to the two-way fixed effects results:
bind_rows(all_coefs_within,
all_coefs_between,filter(all_coefs,Type=="Replication")) %>%
ggplot(aes(y=Estimate,x=Model)) +
geom_pointrange(aes(ymin=lb,ymax=upb,colour=Type),
position=position_dodge(width=.8),
fatten=2) +
geom_text(aes(label=round(Estimate,digits=2),group=Type),
position=position_dodge(width=.8),
size=2.5,vjust=-.75,fontface="bold") +
theme_tufte() +
geom_vline(xintercept=0,linetype=2) +
scale_colour_viridis_d() +
geom_hline(yintercept=0,linetype=2) +
scale_y_continuous(labels=scales::percent_format(scale=1)) +
coord_flip() +
labs(x="Comparison Period",y="Percentage Change in Daily COVID-19 Cases") +
ggtitle(stringr::str_wrap("Comparison of Mask Mandates Effects both Within-County Over-time and Daily Cross-sections",width = 60))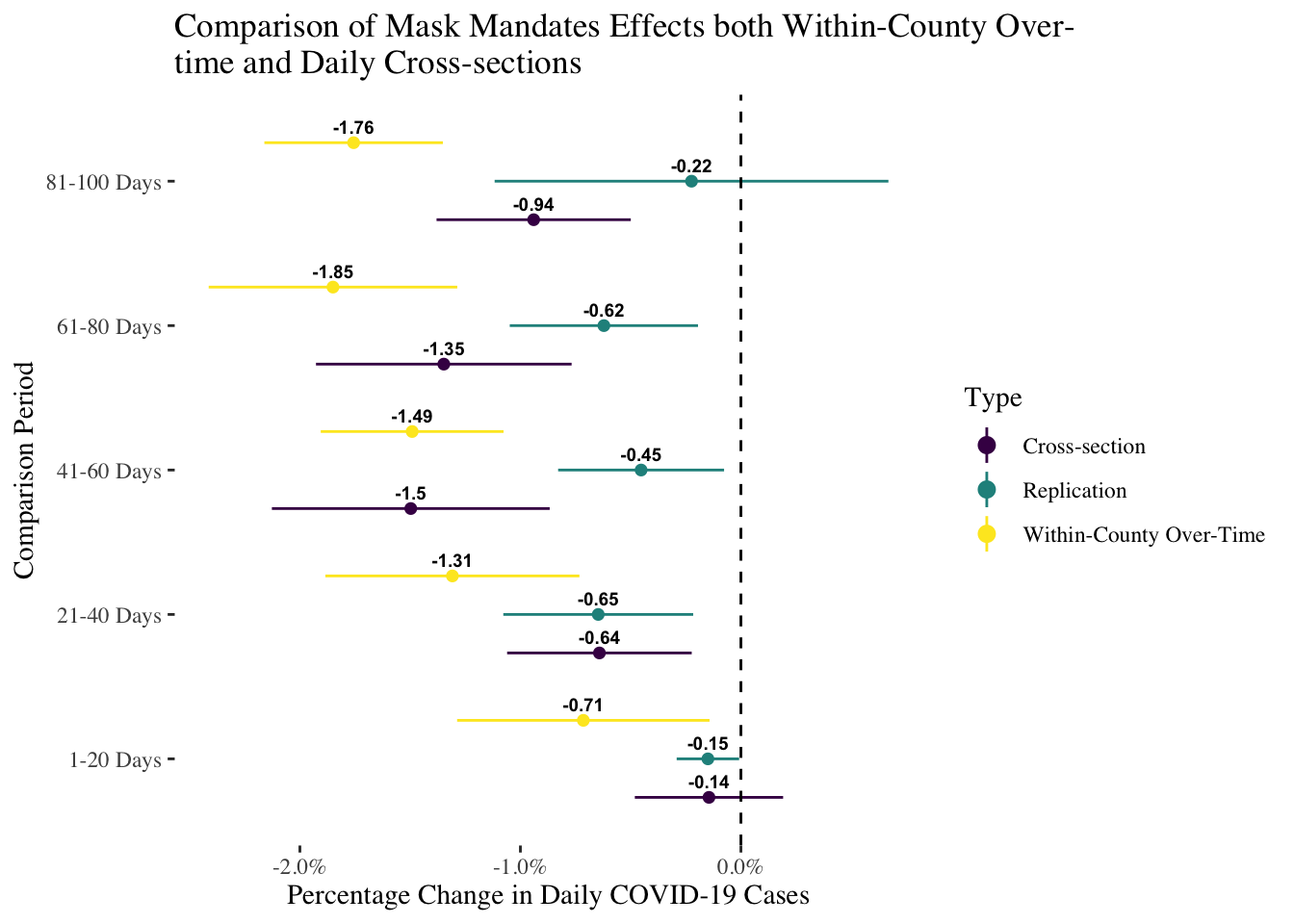
As can be seen, the models with either fixed effects for days or counties tend to have larger and more negative estimates of the effect of mask mandates than do the two-way fixed effects models. This is of course puzzling, as if the two-way fixed effects models controls accounts for both sets of fixed effects, shouldn’t the estimate be somewhere between the two one-way models? That intuition is misleading and deeply flawed. The two-way fixed effects model combines variation in both dimensions in a way that is complex and highly non-linear, which means it could produce an estimate completely independent of both dimensions in the data. That is the reason why that estimate is hard to interpret, and frankly not the best choice for the CDC. I have no idea what the two-way estimates substantively mean–whether and to what extent they refer to variation within counties or variation across counties–and as a result I can’t also explain why they are lower than either considered separately.
How to Do It Better
To summarize the blog post so far, the CDC is trying to take seriously the fact that mask mandates were not randomly assigned to counties, and that the course of the pandemic is affecting counties in a variety of ways over time. However, their approach tries to use brute force modeling and arbitrary data subsetting. There must be a better way, you ask. Well, there is, if we are comfortable with trying first to draw relevant comparisons while acknowledging that in this situation, there probably is no way to easily remove all concerns about other factors that could affect or explain the results. However, we can still do better by addressing these inferential threats head on rather than try to sneak around them with hordes of dummy variables.
As mentioned earlier, there are two basic and much clearer options for panel data models: within-case county models and cross-section by day models. (Later on I will show some new work that offers other options, but we’ll stick with these for now). I chose to go with the cross-sectional models, which may be a bit surprising, but the reason has to do with available data. For the within-county over-time model, we should be concerned about rising awareness of masks and beliefs in their effectiveness. Unfortunately, there is very little over-time data on counties we can use. Most polling is only available at the state level at best. We have Google mobility data by day, but that is about it. If we are concerned that people become more compliant with mask mandates over time because they are becoming better informed about how masks help, there is no way to include data about those changing perceptions in the model.
By contrast, in the cross-sectional model we would need to be worried about a different issues: are there different reasons why some counties would adopt mask mandates in the first place? That is, when we compare counties with and without mask mandates, are there reasons why they adopt mask mandates and see fewer infections? The answer is, of course there are. However, we can measure these factors because they are constant over time. For my purposes, I collected three important control variables: county median income, the proportion foreign-born from the Census, and crucially, 2016 presidential vote totals for Donald J. Trump.
In my own work on the pandemic, which you can read more here, I show that Trump partisanship has a very strong relationship to spread of the pandemic. In that paper I examine states, so I can look at within-state variation because I can measure changes in Trump approval ratings over time. Lacking that data for counties, though, we can still examine whether partisanship affects mask mandates–which we should expect. Counties that are more conservative are probably less likely to adopt mask mandates, and if they do adopt them, to comply with them, while the opposite probably holds true for more liberal areas. Adding in county-level income helps account for the resources a county might have to address the pandemic and also how many workers are exposed to the virus through their daily jobs as we know that higher-paid workers tended to work at home. The proportion of foreign-born is a proxy for travel patterns as foreign residents tend to live closer to areas with access to international travel, which was a cause of the early spread of COVID-19. By accounting for these factors, we can make more compelling comparisons between counties by controlling for the factors that might prompt some counties to be more likely to adopt mask mandates and to see greater levels of compliance.
In the code below, I include the CDC’s data with the additional control variables. I also interact mask mandate status with vote share to see if mask mandates do seem to be more effective in more liberal areas. While it would be nice to include a two-way fixed effects for comparison’s sake, the model could not estimate due to some collinearities between variables (not clear why). Oddly enough, I could estimate such a model when using the smaller subsets of the data that the CDC did. It is really an odd duck.
Following is the code I used to estimate a model with additional controls and fixed effects for days:
d1_part_between <- fixest::feols(
cases_diff_log ~ mask_status*vote_share + scale(test_prop) + vote_share +prop_foreign + scale(median_income) + stay_status + rest_action + bar_order + ban_gather |
date,
data =
combined_data,
cluster =
"FIPS_State",
weights =
~ pop
)In the plot below I show all of the results of the model ordered by how negative or positive their association is with COVID-19 spread. What is immediately apparent is a strong and very positive association between Trump vote share and COVID-19: more conservative areas tend to see more infections after controlling for other factors. Furthermore, removing restrictions on bars is strongly associated with more infections, though we don’t see similar associations for restaurants, which may be a comfort to non-bar restaurant owners and the precautions they’ve taken. Importantly, the interaction effect on Trump vote share and mask mandates is strongly positive, suggesting that mask mandates are less effective in conservative areas.
d1_part_between$coeftable %>%
mutate(Variables=row.names(d1_part_between$coeftable),
Variables=forcats::fct_recode(Variables,
"Ban on >10 Gatherings" = "ban_gather",
"Bars Curbside Only" = "bar_orderCurbside/delivery only",
"No Bar Restrictions" = "bar_orderNo restriction found",
"Bars Open with Limitations" = "bar_orderOpen with limitations",
"Mask Mandate" = "mask_statusPublic Mask Mandate",
"Mask Mandate X Trump Vote" = "mask_statusPublic Mask Mandate:vote_share",
"Median Income" = "scale(median_income)",
"% Foreign" = "prop_foreign",
"Restaurant Curbside Only" = "rest_actionCurbside/carryout/delivery only",
"Restaurant Open with Precautions" = "rest_actionOpen with social distancing/reduced seating/enhanced sanitation",
"Stay at Home Advisory" = "stay_statusAdvisory/Recommendation",
"Stay at Home Mandatory" = "stay_statusMandatory - all people",
"Stay at Home Certain Areas" = "stay_statusMandatory - all people in certain areas of state",
"Stay at Home At-risk Certain Areas" = "stay_statusMandatory - at-risk in certain areas of state",
"Stay at Home At Risk Only" = "stay_statusMandatory - at-risk people only",
"Tests" = "scale(test_prop)",
"Trump Vote" = "vote_share"
)) %>%
ggplot(aes(y=Estimate,x=reorder(stringr::str_wrap(Variables,width = 40),Estimate))) +
geom_pointrange(aes(ymin=Estimate - 1.96*`Std. Error`,
ymax=Estimate + 1.96*`Std. Error`),fatten=2,alpha=0.8) +
geom_text(aes(label=round(Estimate,digits=2)),
size=2.5,vjust=-.75) +
theme_tufte() +
geom_vline(xintercept=0,linetype=2) +
scale_colour_viridis_d() +
scale_y_continuous(labels=scales::percent_format(scale=1)) +
coord_flip() +
labs(y="Percentage Change in COVID-19 Cases",x="") +
ggtitle(stringr::str_wrap("Trump Vote Share Interaction with Mask Mandates",width = 60))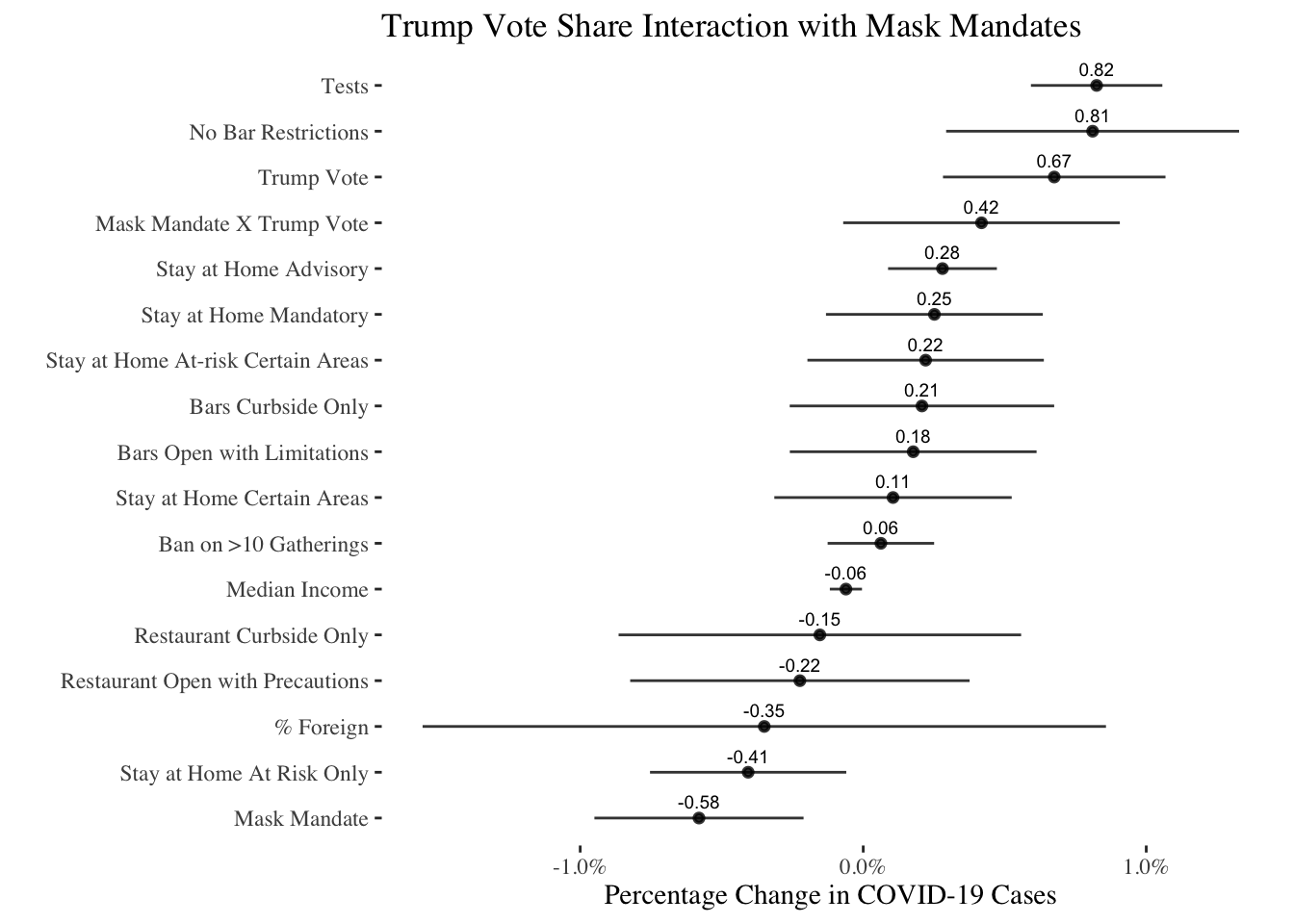
To better understand the relationship between vote share and mask mandates, I plot the sample-average marginal effects for mask mandates below. These estimates show what effect the mask mandate seemed to have across counties when we vary vote share for Donald Trump from the lowest observed value of 4.1% voting for Trump to the maximum value of 96% voting for Trump:
# use Leeper's method for calculating marginal effects
# ignore uncertainty as that would require bootstrapping/jackknifing
eps <- 1e-7
setstep <- function(x) {
x + (max(abs(x), 1, na.rm = TRUE) * sqrt(eps)) - x
}
# loop over full range of vote shares
combined_filter <- ungroup(combined_data) %>%
select(
date,
mask_status,
test_prop,
vote_share,
prop_foreign,
median_income,
stay_status,
rest_action,
bar_order,
ban_gather
) %>%
mutate(test_prop = scale(test_prop),
median_income = scale(median_income)) %>%
filter(complete.cases(.))
over_vote <- parallel::mclapply(seq(
min(combined_filter$vote_share),
max(combined_filter$vote_share),
length.out = 100
),
function(v) {
this_data <- rbind(
mutate(
combined_filter,
vote_share = v,
mask_status = "No Public Mask Mandate"
),
mutate(
combined_filter,
vote_share = v,
mask_status = "Public Mask Mandate"
)
)
# get predictions and take average difference
y_hat <-
predict(d1_part_between, newdata = this_data)
ld <- nrow(combined_filter)
# marginal effect = E[y_hat under treatment - y_hat under
# control] conditional on vote_share = v
marg_eff <-
mean(y_hat[(ld + 1):(2 * ld)] - y_hat[1:ld])
tibble(`Marginal Effect` = marg_eff,
`Vote Share` = v)
}, mc.cores = parallel::detectCores()) %>% bind_rows
over_vote %>%
ggplot(aes(y=`Marginal Effect`,
x=`Vote Share`)) +
geom_line(linetype=2) +
scale_y_continuous(labels=scales::percent_format(scale=1)) +
scale_x_continuous(labels=scales::percent) +
theme_tufte() +
labs(y="Change in Growth Rates",
x="Trump 2016 Vote Share") +
ggtitle("Marginal Effect of Mask Mandates on COVID-19 Growth Rates",
subtitle = "Conditional on 2016 County-level Trump Vote Share")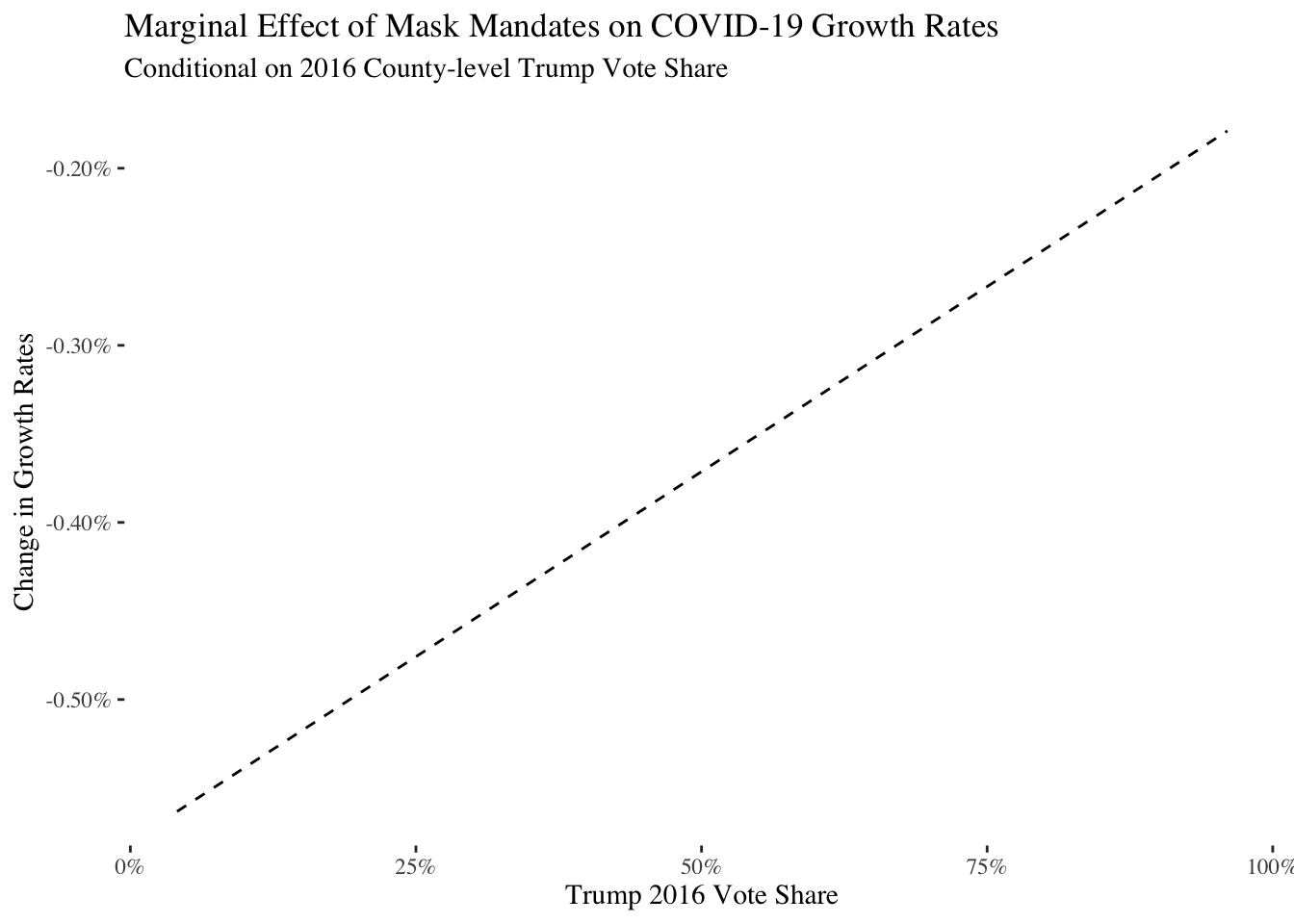
Unfortunately, I don’t have uncertainty for the plot as that would require a lot more work given the fixed effects. However, the relationship is quite strong and clear: mask mandates are most effective in counties that did not vote for Trump and least effective in counties that voted the most for Trump. In those counties, mask mandates are almost ineffective at preventing COVID-19. As a result, it’s clear that the CDC should have included partisanship in their model in some way.
Again, this model is imperfect: there are certainly other factors we might want to include in the model, and there is always the chance that there is some other part of the picture we are missing. Such, however, is life with observational data. We can still learn from these comparisons provided we are appropriately skeptical.
In addition, we could consider using some newer, more nuanced methods. I turn to these next.
Another Way: Multiple Period Diff-in-Diff
Recent research on panel data models has been promoting the use of what is called multi-period difference-in-difference. Difference-in-difference modeling has a big fan base because it seems to draw a compelling and possibly causally identified comparison between units observed at two time periods, pre and post-treatment. Curiously, though few notice it, the comparisons are actually of two cross-sections over time, and so is substantively similar to the cross-sectional model I ran earlier.
However, when there are more than two time periods, or when units are treated at different times, then the simple difference-in-difference model doesn’t apply. There issues are present in spades in the CDC’s analysis: many counties adopted mask mandates at different times and for different lengths of time. The CDC tried to restrict their sample to specific days, to avoid this, but because counties adopted mask mandates on different dates, they inevitably end up comparing different periods as well.
There is increasing research on how best to make a difference-in-difference like comparison in more complicated situations. In this section I use the work of Callaway and Sant’Anna, which has a compelling take on this question. Using their approach, we first assign counties to the same group for comparison if they adopted a mask mandate on the same day. In that way, we might think that some of the over-time issues I mentioned earlier will not matter as much. Second, we can be more up front about what we use as the reference group, either counties that on that day did not have a mask mandate or counties which never imposed a mask mandate. For our purposes, I’ll adopt the former approach given that many counties had a mask mandate at some point. As if that weren’t enough, we can even include what they call anticipation effects, which would occur if people started to change their behavior before the mask mandate was implemented.
In the code below I fit their model to the CDC data with an allowance for anticipation of up to 3 days. The resulting model ends up being gigantic as the 3,000 plus counties are assigned to one of a possible 200+ groups given the number of days. The model also complained that some of our groups were consequently too small, i.e., only a few counties adopted a mask mandate on that particular day. Furthermore, I only include the additional control variables like vote share, not the CDC’s policy data as it is likely to be problematic to include it when the groups are so small. As is always the case, this model is not a panacea for our concerns due to these issues, but we can still learn quite a bit from it.
# takes about 30 minutes to estimate
if(run_did) {
did_est <- combined_data %>%
ungroup %>%
select(cases_diff_log,first_treat,fips_num,date_num,
vote_share,test_prop,prop_foreign,median_income,
stay_status,rest_action,bar_order,ban_gather) %>%
filter(complete.cases(.)) %>%
att_gt(yname="cases_diff_log",
gname="first_treat",
idname="fips_num",
tname="date_num",
xformla=~vote_share + test_prop + prop_foreign + median_income,
# xformla=~vote_share + test_prop +prop_foreign + median_income + stay_status + rest_action + bar_order + ban_gather,
control_group="notyettreated",
anticipation=3,panel=TRUE,allow_unbalanced_panel = F,
cores=4,weightsname = NULL,
est_method="reg",
data=.)
saveRDS(did_est,"data/did_est.rds")
} else {
# File is too big to store on github, to download use this link:
# https://drive.google.com/file/d/18GhUFbcLbx4a27Y5LJ2Ov_Iexn0ws6mb/view?usp=sharing
did_est <- readRDS("data/did_est.rds")
}We then end up with separate estimates for mask mandate for each of the 3,000+ groups. This is cool, though not particularly useful for us. What I like about Callaway and Sant’Anna’s work though is that they are more transparent about the different dimensions of panel data (even if they tend not to use that terminology). Given the group-level estimates, they have a way of aggregating these to an effect of the mask mandate for each day of the sample. I show these in the plot below.
# we need to aggregate and plot these
# some bug in the package requires this to be loaded
library(DRDID)
library(matrixStats)
library(MatrixModels)
ag_did <- aggte(did_est,type="dynamic")
ag_overall <- aggte(did_est,type="group")
ggdid(ag_did) +
theme_tufte() +
theme(axis.ticks.x = element_blank()) +
scale_x_continuous(breaks=c(-200,-100,-50,-25,0,25,50,100,200)) +
geom_hline(yintercept=0,linetype=2) +
xlab("Days Before/After Mask Mandate")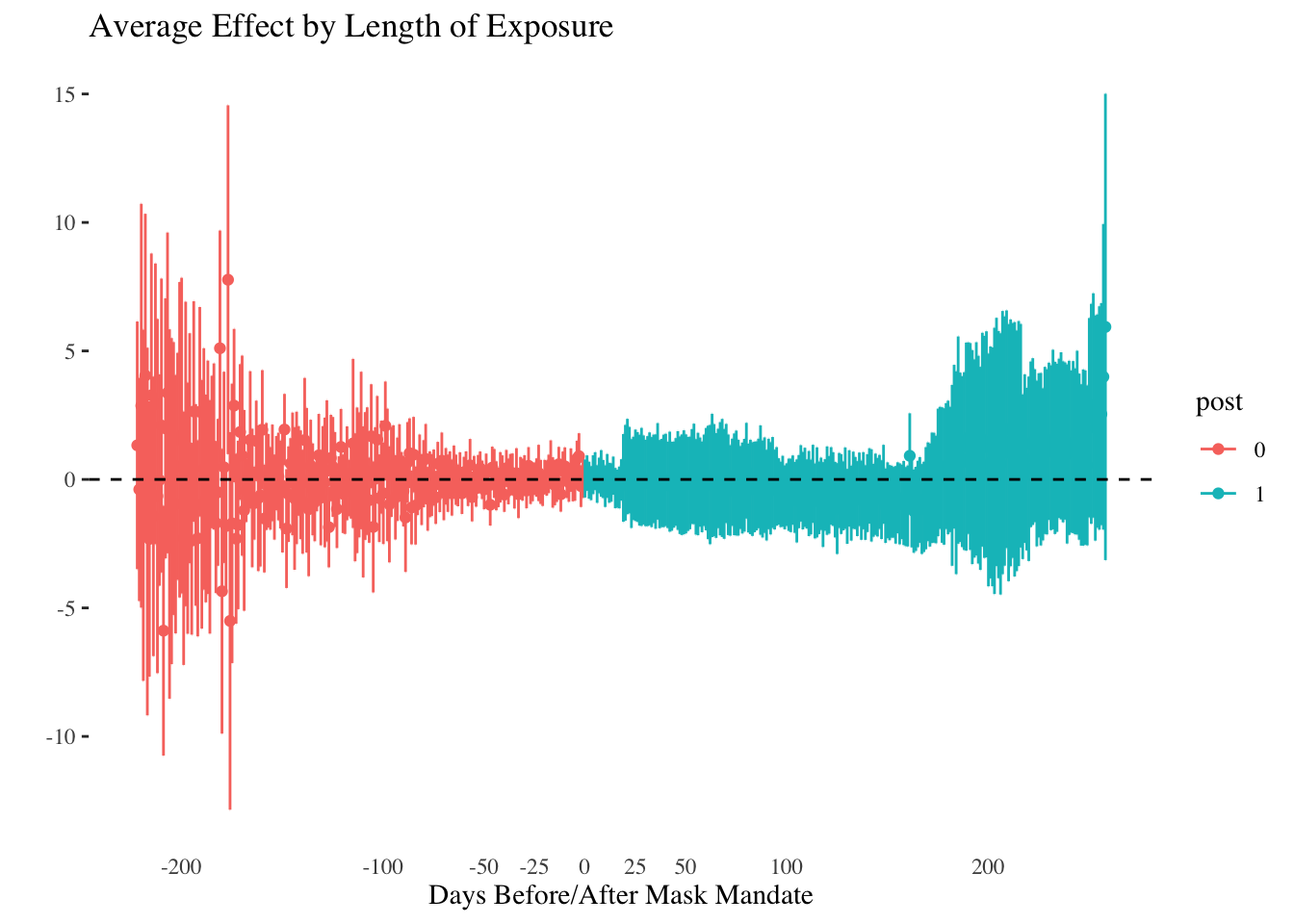
This plot encapsulates a much more nuanced set of comparisons than those considered previously. At the same time, the uncertainty in the estimates means there is also only so much we can learn. It would appear that at earlier and later time periods, mask mandates were associated with more COVID-19, but its impossible to say for sure. One approach to deal with this could be to collapse the data to weeks and then estimate a model, which might pool the data somewhat to get more precise answers.
What we can also do with this model is combine the estimates into a single, overall effect. I show that in the table below.
tibble(`Average Treatment Effect for Treated`=ag_overall$overall.att,
`5% CI Lower`=ag_overall$overall.att - 1.96*ag_overall$overall.se,
`95% CI Upper`=ag_overall$overall.att + 1.96*ag_overall$overall.se) %>%
knitr::kable(digits=2) %>%
kableExtra::kable_styling()| Average Treatment Effect for Treated | 5% CI Lower | 95% CI Upper |
|---|---|---|
| -0.33 | -0.94 | 0.28 |
This table shows that it is most likely there is a negative association for mask mandates with COVID-19: hurrah! Unfortunately, the estimate is fairly imprecise and it could also be associated with increased disease spread. As is so often the case, data analysis does not always produce definitive answers. However, I believe it is most important to be open about what we know and what we don’t know, which is why I spent the time to write this post. On the whole, the evidence suggests a negative association between mask mandates and COVID-19 spread, but we need to do a better job collecting additional data to allow us to do informed comparisons at the county level.