What's Logs Got to Do With It?

Simulation

I next use simulations to discuss this issue to show practically what the authors are talking about and also demonstrate how ordbetareg can estimate scale-free ATEs.

I simulate data that matches what the articles discuss: highly skewed outcomes with zeroes. To do so I’ll simulate a two-part or hurdle model in which the ATE influences the first part (the probability of a 0) and the second part (a conventional log-normal distribution strictly greater than 0). The ATE will influence both the probability of 0s, which at baseline is 10% of total observations, and the mean of the non-0 (log-normal) distribution. I will assume a true ATE of +1 on the log/logit scale. I can then simulate the potential outcomes, Y1 and Y0, as independent distributions with a difference of the ATE.

ate <- 1
N <- 500
Y0 <- ifelse(runif(N)<0.9,rlnorm(N),0)
Y1 <- ifelse(runif(N)<plogis(qlogis(0.9) + ate),
             rlnorm(N,meanlog=ate),
             0)

We can take a quick glance at the distributions:

hist(Y1)

hist(Y0)

The proportion of zeroes in Y0 is 0.086 and the proportion of zeroes in Y1 is 0.034.

We can then do some conventional comparisons of the treatment and control group, a t-test and linear model fit:

t.test(Y1,Y0)

## 
##  Welch Two Sample t-test
## 
## data:  Y1 and Y0
## t = 11.45, df = 639.8, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  2.423978 3.427505
## sample estimates:
## mean of x mean of y 
##  4.330918  1.405176

t_data <- tibble(Y=c(Y0,Y1),T=c(rep(0,N),rep(1,N)))
mod1 <- lm(Y ~ T,data=t_data)
summary(mod1)

## 
## Call:
## lm(formula = Y ~ T, data = t_data)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -4.331 -1.839 -0.795  0.423 48.338 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.4052     0.1807   7.777 1.84e-14 ***
## T             2.9257     0.2555  11.450  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.04 on 998 degrees of freedom
## Multiple R-squared:  0.1161, Adjusted R-squared:  0.1152 
## F-statistic: 131.1 on 1 and 998 DF,  p-value: < 2.2e-16

The linear model and the t-test do not return the true ATE as that was simulated on the log scale. However, if we take the log of the estimate, it is pretty close – log of 2.926 is 1.074. The simulation is not perfect because the ATE will vary across the two parts due to scaling effects, but it will work for our purposes.

As the papers pointed out, the ATE could change if we use nonlinear transformations such as log with an adjustment such as 1 or 0.1 to replace the zeroes. We will test this by fitting two models, one with an outcome of \(log(Y+1)\) and the other with \(log(Y+0.01)\). We can then make a table of the model results with the modelsummary package:

t_data <- mutate(t_data,
                 Y_1=Y + 1,
                 Y_01=Y + 0.01)

y_mod1 <- lm(log(Y_1) ~ T,data=t_data)
y_mod2 <- lm(log(Y_01) ~ T, data=t_data)

modelsummary(models=list(`log(Y + 1)`=y_mod1, 
                         `log(Y + 0.01)`=y_mod2))

We can see that the treatment effects are quite different. To get them back on the same scale, we can try a reverse transform (exponential the coefficient):

exp(coef(y_mod1)[2]) - 1

##         T 
## 0.9159342

exp(coef(y_mod2)[2]) - .01

##        T 
## 3.433134

We can see that the reverse transform doesn’t improve matters. In either case we end up with a very different coefficient. If we were to interpret the outcome as dollars, such as a salary, then the ATE in the first model would be 0.92 and the ATE in the second would be 3.28. As the papers suggest, changing that constant results in changes in the ATE, and so we need to be careful what constant we choose.

To see if units matters as the papers also propose, we will divide the outcome by 100 and compare to the original outcome while using the same transformation of \(log(Y + 1)\):

t_data <- mutate(t_data,
                 Y_1_rescale=(Y/100)+1)

y_mod1_rescale <- lm(log(Y_1_rescale) ~ T,data=t_data)

modelsummary(models=list(`log(Y + 1) Original`=y_mod1, 
                         `log(Y + 1) Rescaled`=y_mod1_rescale))

Again, we can see that rescaling \(Y\) and then applying the \(log(Y+1)\) transformation results in a remarkably different ATE. Because dividing by a constant doesn’t affect the proportion of zeroes but does affect the non-zero values, the ATE will consequently change when using this transformation.

ordbetareg to the Rescue

While the authors propose some solutions to this problem, such as using a two-part model, I want to show that the ordered beta regression can estimate scale-free ATEs if the outcome is normalized; that is, rescaled to between 0 and 1. Here we will let 0 be equal to 0 while 1 will be the sum of the outcome, i.e., the total income of the sample. We can rescale so that each observation in our data is equal to the proportion of the total. It corresponds to the following estimand, which I’ll call \(ATE_n\) for normalized:

\[ ATE_n = E[\frac{Y1}{Y1+Y0} - \frac{Y0}{Y1+Y0}] \]

Crucially, if we scale the outcome by any value \(c\), \(c\) will cancel as it will be in both the top and bottom of the fraction. We could estimate this quantity with either OLS or a t-test, but the error term is likely to be misleading as it won’t respect the bounds of the outcome (i.e. 0 or 1). This is where ordered beta regression can help. I’ll estimate two models, one with the original outcome and the second with the original outcome multiplied by a 100 to test for scaling effects. I will specify the true_bounds parameter to be 0 and 1 as by definition there will not be any values at the upper bound of 1.

t_data <- mutate(t_data,
                 Y_n=Y/(sum(Y)),
                 Y_n_rescale=(Y/100)/(sum(Y/100)))

y_n_mod <- ordbetareg(Y_n ~ T,data=t_data,
                      chains=1,iter=1000,
                      true_bounds=c(0,1),refresh=0,
                      backend="cmdstanr")

## Running MCMC with 1 chain...
## 
## Chain 1 finished in 3.3 seconds.

y_n_rescale <- ordbetareg(Y_n_rescale ~ T,data=t_data,
                          chains=1,iter=1000,
                          true_bounds=c(0,1),refresh=0,
                          backend="cmdstanr")

## Running MCMC with 1 chain...
## 
## Chain 1 finished in 3.5 seconds.

modelsummary(models=list(`Normalized Y Original`=y_n_mod, 
                         `Normalized Y Rescaled`=y_n_rescale),
             statistic="conf.int")

As can be seen, both estimates are very close. We can convert these treatment effects to marginal effects using the marginaleffects package:

margin_Y <- marginaleffects(y_n_mod, variables="T")
summary(margin_Y)

##   Term    Effect    2.5 %   97.5 %
## 1    T 0.0009132 0.000636 0.001788
## 
## Model type:  brmsfit 
## Prediction type:  response

The treatment effect here is miniscule as it represents the proportion of income in the sample accruing to an individual unit. However, we can transform this back to the original scale by simply multiplying the estimated marginal effect for each posterior draw by the sum of Y1 and Y0:

treatment <- posteriordraws(margin_Y) %>% 
  distinct(draw) %>% 
  mutate(T=draw * sum(t_data$Y))

# calculate a summary/point estimate
summary(treatment$T)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.191   1.814   2.623   2.830   3.468   8.645

# plot full distribution/uncertainty
hist(treatment$T)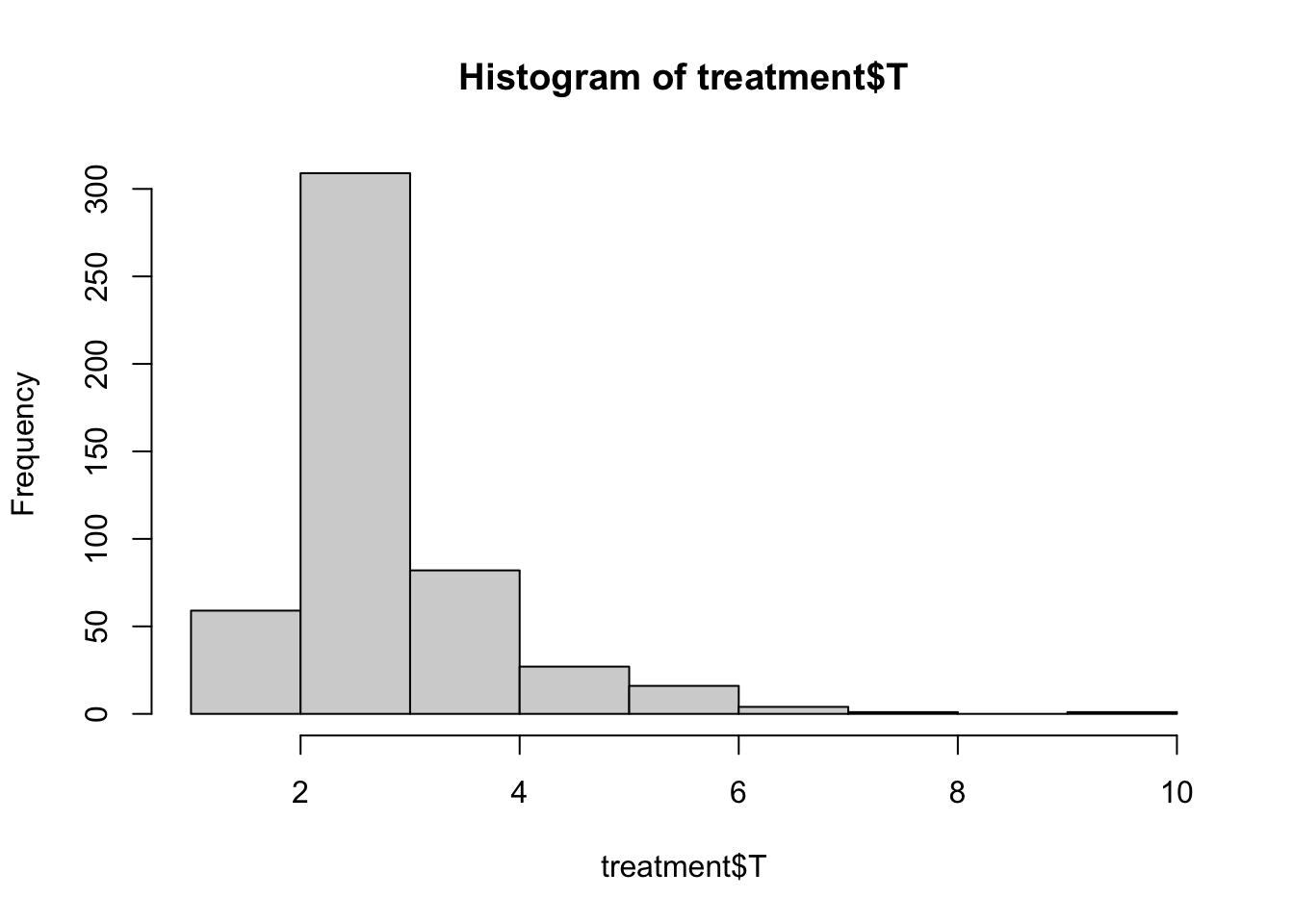

Doing so gives us a treatment effect of approximately $2.7 dollars on the original scale–or, almost exactly \(log 1\) as per our original true ATE. Importantly, the estimated uncertainty of this ATE, which we can visualize by plotting all the posterior draws as a histogram, reflects the skew of the underlying variable, which in this case we would want to capture.

As the package designer Vincent Arel-Bundock pointed out, I can also do the code above using the marginaleffects package directly with the comparisons function:

treatment2 <- comparisons(y_n_mod,
                          variables="T",
                          transform_pre="dydx",
                          transform_post=function(x) x * sum(t_data$Y)) %>% 
  summary

print(paste0("The treatment effect estimate is ",
             round(treatment2$estimate,3),
             " with a lower bound of ",
             round(treatment2$conf.low,3), 
             " and an upper bound of ",
             round(treatment2$conf.high,3),"."))

## [1] "The treatment effect estimate is 2.619 with a lower bound of 1.824 and an upper bound of 5.128."

Conclusion

For these reasons, ordbetareg can be used to produce ATEs that are scale-free yet can be still be back-transformed to the original scale by rescaling the marginal effects as produced by the marginaleffects package. If the aim of the analysis is to estimate an ATE that is comparable across samples and income distributions, yet also doesn’t lose its relation to the original data, then ordbetareg can provide readily comparable estimates.